PROGRAMA PARA EL ANÁLISIS DEL COMPORTAMIENTO

PROGRAMA PARA EL ANÁLISIS DEL COMPORTAMIENTO

ÓPTIMO DE UNA RED ELÉCTRICA

PERCY ARIEL GARRIDO ZÚÑIGA

Ingeniero Eléctrico y Electrónico

RESUMEN

El alto costo de producción de energía, la competitividad de las tarifas y las frecuentes regulaciones, hacen que sea fundamentalmente importante alta eficiencia en la producción de energía, para poder obtener las mejores ganancias.

Procurar mayor eficiencia no es simplemente concentrar funcionamiento en las unidades de mayor eficiencia. En el suministro de energía eléctrica se debe procurar cubrir la carga al más bajo costo posible por cada MW, Esto se logra al poner a funcionar todas las unidades disponibles en el mismo punto de costo incremental efectivo (Ci =Ci ₁ =Ci ₂, ... ,=Ci _n).

Una vez obtenido un despacho económico y utilizando un análisis de flujo de potencia conjugado con algunas fórmulas simples, se pueden obtener los parámetros del punto óptimo de funcionamiento de cada uno de los componentes de una red eléctrica.

Debido al gran tamaño de las redes eléctricas y al dinámico comportamiento de una carga real, es recomendable utilizar un buen programa de computadora para el análisis del comportamiento óptimo de la red.

PALABRAS CLAVES: Análisis de flujo de potencia, despacho económico, punto óptimo de operación, método Gauss-Seidel, método Newton-Raphson.

INTRODUCCIÓN

Los estudios de flujo de potencia son de gran importancia en el planeamiento y diseño de la expansión futura de los sistemas de potencia, así como en la determinación de las mejores condiciones de operación de los sistemas existentes. La naturaleza de los métodos de cálculos utilizados para este fin y además la común complejidad de las redes eléctricas existentes requiere el uso de paquetes o programas de computadoras.

La operación económica de un sistema de potencia es de muy importante para recuperar y obtener beneficios del capital que se invierte. Las tarifas que fijan las instituciones reguladoras y la importancia de conservar el combustible presionan a las compañías generadoras para alcanzar la eficiencia máxima posible. La máxima eficiencia minimiza el costo de Kilowatthora (KWh) a los consumidores pues reduce el costo que representa a la compañía el suministro de este HWh.

Para cualquier condición de carga especificada, el despacho económico determina la salida de potencia de cada unidad generadora que minimiza el costo total necesario para alimentar la carga del sistema.

Al combinar el despacho económico con el análisis de flujo de potencia se pueden obtener los datos de una red eléctrica que funciona óptimamente.

FUNDAMENTO TEÓRICO

Flujo de Potencia

Cualquier red eléctrica puede representarse con un sistema de ecuaciones propio, por tal motivo lo más importante es utilizar un método numérico apropiado para resolverlo.

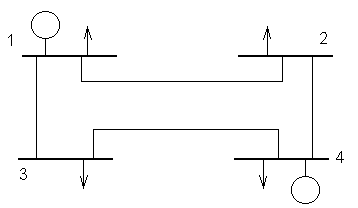
Por conveniencia en el análisis de Flujo de Potencia se toma una de las barras (nodo) de la red como la de compensación; esta barra sirve como referencia para los valores de todas las demás barras. Entonces, no hay necesidad de incluir la ecuación de esta barra en el análisis.

Aplicado al Análisis del Flujo de Potencia con el Método Gauss- Seidel

Es evidente que un sistema de 4 barras, en donde la barra 1 es la de compensación, requiere solo de 3 ecuaciones para su completa definición.

Haciendo uso de la Ley de Ohm (V=IR) y la definición de potencia compleja (S=VI^*) se puede decir que:

, o en forma matricial:

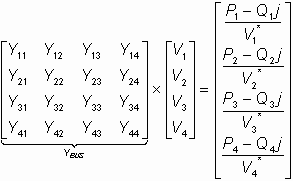
Como el nodo 1 es la barra de compensación, el sistema de ecuaciones queda de la siguiente forma:

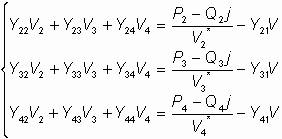
En este punto se puede aplicar el método numérico de Gauss-Seidel para resolver este sistema de ecuaciones lineales y obtener los valores de voltaje (módulo y ángulo) en cada nodo de la red.

La experiencia con el método Gauss-Seidel para la solución de Flujo de Potencias ha mostrado que se puede reducir el número de iteraciones requeridas si el valor absoluto de la diferencia de voltajes de dos iteraciones sucesivas se multiplica por alguna constante. El multiplicador que lleva a cabo esta convergencia mejorada se llama factor de aceleración(a ).

La elección del factor de aceleración adecuado a menudo se determina por tanteo. En general es innecesario para la solución del sistema, sin embargo, como generalmente en el análisis de flujo de potencia los sistemas bajo estudio se resuelven varias veces, puede ser de gran importancia una buena elección del factor de aceleración.

Aplicado al Análisis del Flujo de Potencia con el Método Newton- Raphson

La fórmula de Newton Raphson:

se pude expresar de la siguiente forma:

Generalizando para varias variables y en forma matricial, se tiene:

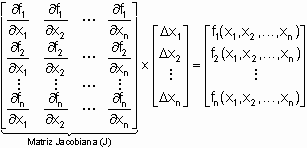
Si la matriz Jacobiana es trasladada al lado derecho de la ecuación, se pueden obtener los incrementos entre iteraciones de cada una de las incógnitas.

Nuevamente, por la ley de Ohm y la definición de potencia compleja en una barra i, se pude decir que:

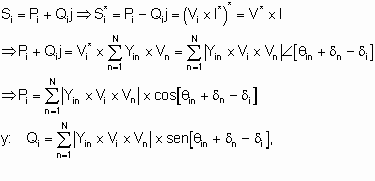
en donde las incógnitas son: d _ny V_n con n=1,2,...,N y N es la cantidad de nodos de la red.

A excepción de la barra de compensación, cada uno de los nodos es representado por una ecuación de P y su correspondiente de Q.

Al juntar todas las ecuaciones se puede aplicar el método de Newton-Raphson para resolver este sistema no lineal y obtener los valores de voltajes (módulo y ángulo) en cada nodo de la red.

Debido a que una variación en el ángulo del voltaje no afecta, en gran medida, la potencia reactiva (Q) y a que un cambio en el módulo del voltaje no afecta en gran medida la potencia real (P), se puede decir que:

Este hecho, que representa el concepto del Método Desacoplado, reduce, significativamente, los cálculos necesarios para la matriz Jacobiana, obteniendo una muy eficiente aproximación al considerar nulos los términos en los que se puede aplicar esta suposición.

Cuando se resuelve un sistema de transmisión de gran escala, el Método Desacoplado de flujo de potencia representa una buena alternativa para reducir el tiempo de cálculo.

Cálculo de Más Detalles de la Red

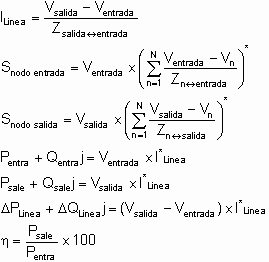
Una vez obtenido los valores de los voltajes de cada nodo de la red, se puede obtener más información haciendo uso de algunas fórmulas simples:

Despacho Económico

Al representar gráficamente el Costo por Megawatthora en función de la Potencia de Salida del funcionamiento de una unidad generadora, se puede observar que su comportamiento es bastante lineal, por lo que muchas veces se puede utilizar la ecuación de la recta para expresarlo.

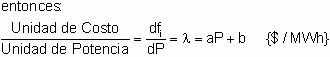
Supóngase un sistema de dos unidades generadoras, en donde una tiene un costo por MWh (l ) más caro que la otra. Al transferir una parte de la carga de la unidad de más alto costo a la de más bajo costo por MWh, la cantidad de dinero que se economiza es mayor que la que se necesitaría para cubrir la misma cantidad de carga, pero añadida a la unidad de más bajo costo incremental. Con la finalidad de economizar aún más, se puede continuar transfiriendo carga de una unidad a la otra hasta que los costos incrementales de ambas unidades sean iguales. Es decir, hasta que las dos unidades, en conjunto, produzcan cada MWh tan barato como les sea posible.

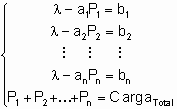
Para encontrar, rápidamente, el costo incremental al que deben trabajar todas las unidades y la potencia generada por cada una de ellas, se puede utilizar el siguiente sistema de ecuaciones:

donde las incógnitas son: l , P₁ , P₂, …, P_n.

Se puede aplicar el método numérico de Newton-Raphson o preferiblemente el método Gauss-Seidel para resolver este sistema de ecuaciones lineales y obtener los valores de potencias y costo incremental al que debe trabajar cada unidad generadora de la red para procurar un despacho económico.

Si al resolver el sistema se obtiene algún valor de potencia que sobrepasa el limite de operación de alguna unidad, entonces esta unidad debe hacerse funcionar en el punto limite en cuestión. Debido a que dicha unidad debe ser fijada a un valor de potencia conocido, se puede obtener directamente de su fórmula, el costo incremental al cual va a trabajar.

Luego de esto, es necesario ejecutar nuevamente los cálculos pero sin considerar la unidad fijada, ni la parte de la carga total que esta cubre. Este ciclo se repite hasta que se obtenga un despacho que cumpla con todos los limites de operaciones de las unidades. Si no se logra cumplir con esto entonces el sistema no tiene despacho económico.

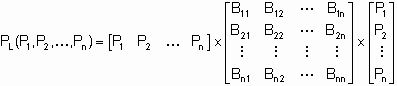
Comúnmente para considerar las pérdidas en una red se utiliza la matriz de coeficientes de pérdida o coeficientes de B. Al multiplicar la matriz (1 x n) de Potencia de las unidades por la matriz de coeficiente B y luego por la matriz (n x 1) de potencia de las unidades, se obtiene la pérdida total (P,) en el sistema.

El costo total de operación se define como:

El balance de potencia en un sistema con pérdidas se puede expresar así:

Si se utiliza el multiplicador de Lagrange X, para minimizar el costo de operación de un sistema (en función de i. y de las salidas de las unidades generadoras) sujeto a la restricción dada por el balance de potencia, se puede decir que:

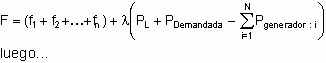
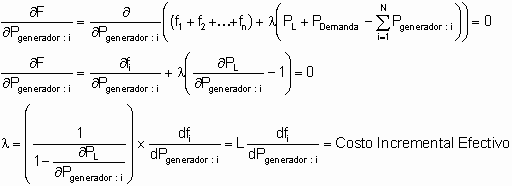
Entonces, se puede afirmar que para considerar las pérdidas en una red eléctrica se debe representar la misma mediante el siguiente juego di ecuaciones:

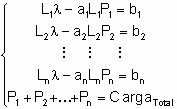
PROGRAMACION EN UNA MINICOMPUTADORA HP-48 SERIE G

El Programa que Analiza el Comportamiento Óptimo de una Red Eléctrica se ha implementado en una minicomputadora HP-48 serie G que proporciona la comodidad de que toda esta capacidad de análisis pueda llevarse en un bolsillo.

Se ha hecho esta selección debido a que en una HP-48 se combina un lenguaje completo y poderoso (Lenguaje Polaco Inverso, RPL) con una forma muy práctica de manipulación de números complejos, matrices reales o complejas y la derivación o integración de funciones, entre otras cosas.

La alta velocidad de cálculo de la HP-48 serie G, su conveniente forma de presentación de datos y la simplicidad de su programación, son también incentivos para su selección.

ALGORITMO E IMPLEMENTACIÓN DEL PROGRAMA

Existe gran similaridad entre muchos tramos en los procedimientos que se deben seguir para el análisis del flujo de potencia y el cálculo del despacho económico, por lo que se ha confeccionado un paquete funcional compuesto por varios sub-programas, para evitar repeticiones innecesarias de listados de instrucciones.

Ya que se utilizan los métodos numéricos de Gauss-Seidel y Newton- Raphson, resulta sencillo y beneficioso procurar que el paquete funcional cuente con la capacidad de utilizar tales métodos, únicamente, para resolver sistemas de ecuaciones. De igual forma, puesto que para el análisis de flujo de potencia se describe la red utilizando la matriz Ysus, se dotó al paquete con una opción para obtener esta matriz de un sistema eléctrico cualquiera. Siendo esto así el paquete cuenta con las siguientes opciones:

· Obtención de matriz Ysus de una red (Y_BUS).

· Método numérico de Gauss-Seidel (G&S).

· Método numérico de Newton-Raphson (N&R).

· Análisis de flujo de potencia con Gauss-Seidel (Pot G&S).

· Análisis de flujo de potencia con Newton-Raphson (Pot N&R).

· Despacho Económico.

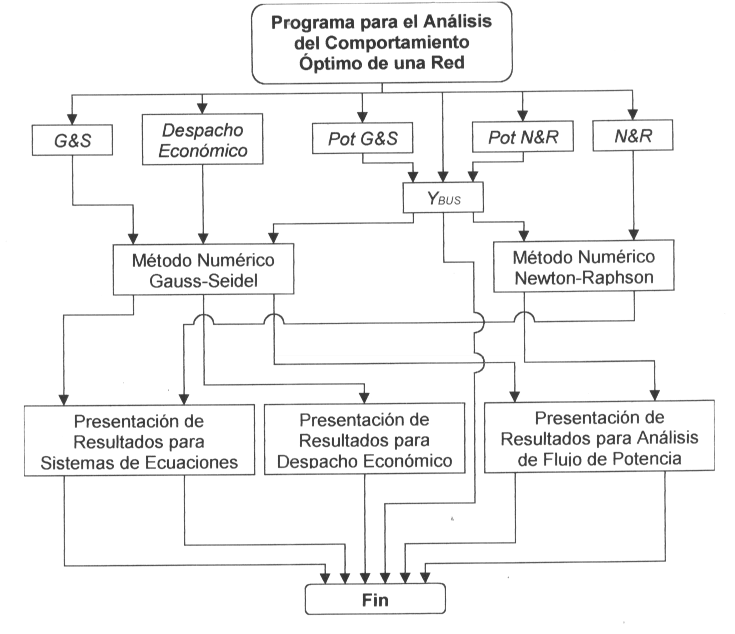
Las opciones de Análisis de flujo de potencia (Pot G&S y Pot N&R) necesitan calcular inicialmente la matriz Y_BUS para obtener sus sistemas de ecuaciones. Las opciones G&S, Pot G&S y el Despacho Económico utilizan el mismo método numérico (Gauss-Seidel) para resolver los sistemas de ecuaciones. Igual ocurre con las opciones N&R y Pot N&R con el método numérico de Newton-Raphson. Resueltos los sistemas de ecuaciones las opciones G&S y N&R siguen iguales procedimientos para la representación de los datos obtenidos. Lo mismo sucede con las opciones de análisis de Flujo de potencia (Pot G&S y Pot N&R) para el "Cálculo de Más Datos de la Red". Mientras que, por su naturaleza, la opción de Despacho económico sigue su propio camino.

CONCLUSIÓN

El Programa POT II para el Análisis del Comportamiento Óptimo de una Red Eléctrica ha sido elaborado utilizando todos los fundamentos aquí explicados.

El programa POT, II que actualmente está siendo utilizado por estudiantes y profesores del último año de la carrera de Ingeniería Electromecánica e Ingeniería Eléctrica y Electrónica de la Universidad Tecnológica de Panamá, ha tenido una gran acogida y muy buenas críticas gracias a su velocidad, fácil utilización, eficiencia, flexibilidad, seguridad y poder.

Para lograr reunir todas estas cualidades se ha puesto mucho cuidado en las instrucciones utilizadas para la confección del algoritmo, procurando un programa, lo más rápido posible, sin aumentar innecesariamente su tamaño. Aprovechando la estructura modular del programa y con la finalidad de reducir su tamaño se han utilizado técnicas de compresión de datos.

El programa POT II y más información sobre el modo de utilización y entorno, están disponibles en Internet en la dirección http://www.percy.cjb.net.

BIBLIOGRAFÍA

· John J. Grainger y William D. Stevenson Jr., "Análisis de Sistemas de Potencia". Editorial McGraw-Hill. México, 1996.

· H. W. Dommel y W.F. Tinney, "Optimal Power-Flow Solutions". IEEE, 1996.

· Steven C. Sharpa y Raynold P. Canale, "Métodos Numéricos para Ingenieros con Aplicaciones en Computadoras Personales". Editorial McGraw-Hill. México, 1998.

· Francis Scheid, "Análisis Numérico". Editorial McGraw-Hill. México, 1988.

· Louis Leithold, "El Cálculo con Geometría Analítica". Editorial Harla. México, 1990.

· Hewlett-Packard Co., "Guia de Usuario de la Calculador HP-48G". E.E.U.U., 1994.

REGRESAR